Python在科研中的应用 07：Python 环境下的数字图像分析方法

Posted on Edited on In Waline:

Python的图像分析方法是一种强大的数据处理技术，它利用多种算法和工具来提取、处理和分析图像数据。通过Python，我们可以方便地调用各种图像处理库，如OpenCV、PIL(Pillow)、SciPy等，进行图像的预处理、特征提取、图像分割、边缘检测等操作。此外，利用Python的机器学习库，如scikit-learn、TensorFlow等，我们还可以对图像进行更高级的分析，如目标检测、图像识别、图像分类等。SciPy是构建在Python的NumPy扩展上的数学算法和便利函数的集合。它通过向用户提供用于操作和可视化数据的高级命令和类，为交互式Python会话添加了强大的功能。有了SciPy，交互式Python会话将成为可与MATLAB、IDL、Octave、R-Lab和SciLab等系统相媲美的数据处理和系统原型环境。

Python的数字图像分析方法章节将持续3-4周的课程，包括数字图像的基础操作，图像降噪，图像分割，边缘检测，目标检测等等。本节课程我们将学习Python在数字图像分析领域的一些基础方法。

Pillow 与 PIL 库

PIL (Python Imaging Library) 是Python平台上图像处理的标准库，功能丰富，API简单易用，不过只支持到Python 2.7。

PIL官方网站：http://www.pythonware.com/products/pil/

Pillow是PIL的一个派生分支，但如今已经发展成为比PIL本身更具活力的图像处理库。

Pillow的Github主页：https://github.com/python-pillow/Pillow
Pillow的文档(对应版本v3.0.0)：https://pillow.readthedocs.org/en/latest/handbook/index.html

给Python安装Pillow非常简单，使用pip或easy_install只要一行代码即可。

1
2
3
4
# 在命令行使用PIP安装：
pip install Pillow
# 或在命令行使用easy_install安装：
easy_install Pillow

安装完成后，使用from PIL import Image就引用使用库了。如：

1
2
3
from PIL import Image
im = Image.open("im.png")
im.rotate(45).show()

使用 Image 类

PIL最重要的类是 Image class, 你可以通过多种方法创建这个类的实例；你可以从文件加载图像，或者处理其他图像, 或者从 scratch 创建。

要从文件加载图像，使用 open() 函数， 在 Image 模块:

1
2
from PIL import Image
im = Image.open("im.png")

加载成功将返回一个 Image 对象。 你现在可以使用示例属性检查文件内容:

1
2
3
from __future__ import print_function
print(im.format, im.size, im.mode)
# PNG (512, 512) RGB

format 这个属性标识了图像来源。如果图像不是从文件读取它的值就是None。size属性是一个二元tuple，包含width和height（宽度和高度，单位都是px）。 mode 属性定义了图像通道的数量和名称，以及像素类型和深度。常见的modes 有 “L” (luminance) 表示灰度图像, “RGB” 表示真彩色图像, 以及 “CMYK” 表示出版图像。

如果文件打开错误，返回 IOError 错误。

只要你有了 Image 类的实例，你就可以通过类的方法处理图像。比如，下列方法可以显示图像:

1
im.show()

标准的 im.show() 效率并不高，它需要保存图像到临时文件然后通过 xv 显示图像。你需要先安装 xv ，显示图像有助于调试和测试。

读写图像

PIL 模块支持大量图片格式。使用在 Image 模块的 open() 函数从磁盘读取文件。你不需要知道文件格式就能打开它，这个库能够根据文件内容自动确定文件格式。

从文件读取

1
2
fp = open("im.png", "rb")
im = Image.open(fp)

从指定路径读取

1
2
3
4
from PIL import Image
import os

im = Image.open(os.path.join(os.getcwd(),"im.png"))

要保存文件，使用 Image 类的 save() 方法。保存文件的时候文件名变得重要了。除非你指定格式，否则这个库将会以文件名的扩展名作为格式保存。

转换文件格式到JPEG

1
2
3
4
5
6
7
8
9
10
11
12
from __future__ import print_function
import os, sys
from PIL import Image

for infile in sys.argv[1:]:
    f, e = os.path.splitext(infile)
    outfile = f + ".jpg"
    if infile != outfile:
        try:
            Image.open(infile).convert('RGB').save(outfile)
        except IOError:
            print("cannot convert", infile)

argv是sys模块的一个全局变量，也称sys模块的一个属性！argv本身为一个list类型的对象，该对象持有的第1个元素是命令行中传入的模块名、从第2个元素开始（含），均为命令行中传入的参数！

注意：argv持有的每个元素的类型均为str（字符串）

save() 方法的第二个参数可以指定文件格式，如果你使用非标准的扩展名你必须这样做：

创建 JPEG 缩略图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from __future__ import print_function
import os, sys
from PIL import Image

size = (128, 128)

for infile in sys.argv[1:]:
    outfile = os.path.splitext(infile)[0] + ".jpg"
    if infile != outfile:
        try:
            im = Image.open(infile)
            im.thumbnail(size)
            im.convert("RGB").save(outfile, "JPEG")
        except IOError:
            print("cannot create thumbnail for", infile)

很重要的一点是这个库不会直接解码或者加载图像栅格数据。当你打开一个文件，只会读取文件头信息用来确定格式，颜色模式，大小等等，文件的剩余部分不会主动处理。这意味着打开一个图像文件的操作十分快速，跟图片大小和压缩方式无关。下面是一个简单的脚本用来快速验证大量图片。

验证图像文件

1
2
3
4
5
6
7
8
9
10
from __future__ import print_function
import sys
from PIL import Image

for infile in sys.argv[1:]:
    try:
        with Image.open(infile) as im:
            print(infile, im.format, "%dx%d" % im.size, im.mode)
    except IOError:
        pass

图像剪切，粘贴，合并，几何变换等

Image 类包含的方法允许你操作图像部分选区。使用:py:meth:~PIL.Image.Image.crop 方法获取图像的一个子矩形选区。

从图像中复制出一个矩形选区

1
2
box = (100, 100, 400, 400)
region = im.crop(box)

矩形选区有一个4元元组定义，分别表示左、上、右、下的坐标。这个库以左上角为坐标原点，单位是px，所以上诉代码复制了一个 300x300 pixels 的矩形选区。这个选区现在可以被处理并且粘贴到原图。

处理复制的矩形选区并粘贴到原图

1
2
region = region.transpose(Image.ROTATE_180)
im.paste(region, box)

当你粘贴矩形选区的时候必须保证尺寸一致。此外，矩形选区不能在图像外。然而你不必保证矩形选区和原图的颜色模式一致，因为矩形选区会被自动转换颜色（参看下面的 颜色变换 部分），下面是一个例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Rolling an image
def roll(image, delta):
    "Roll an image sideways"

    xsize, ysize = image.size

    delta = delta % xsize
    if delta == 0: return image

    part1 = image.crop((0, 0, delta, ysize))
    part2 = image.crop((delta, 0, xsize, ysize))
    image.paste(part2, (0, 0, xsize-delta, ysize))
    image.paste(part1, (xsize-delta, 0, xsize, ysize))

    return image

分离和合并颜色通道

1
2
r, g, b = im.split()
im = Image.merge("RGB", (b, g, r))

注意，对于单通道图像，split()返回图像本身。

几何变换

PIL.Image.Image类包含了resize()和rotate()方法。前者接受一个元组，给出新的大小，后者接受以逆时针为单位的角度。

1
2
3
out = im.resize((128, 128))
out = im.rotate(45) # degrees counter-clockwise
im1 = im1.rotate(90, PIL.Image.NEAREST, expand = 1)

要以90度的步骤旋转图像，您可以使用rotate()方法或transpose()方法。后者也可用于围绕其水平或垂直轴翻转图像。

1
2
3
4
5
out = im.transpose(Image.FLIP_LEFT_RIGHT)
out = im.transpose(Image.FLIP_TOP_BOTTOM)
out = im.transpose(Image.ROTATE_90)
out = im.transpose(Image.ROTATE_180)
out = im.transpose(Image.ROTATE_270)

transpose()方法和相应的rotate()方法在性能和结果上没有区别。

颜色变换

Python成像库允许您使用convert()方法在不同色彩表示之间转换图像。

1
im = Image.open("im.png").convert("L")

该库支持每种受支持的模式与“L”和“RGB”模式之间的转换。要在其他模式之间进行转换，可能必须使用中间图像(通常是“RGB”图像)。

随堂练习

构建一张PNG格式图像，读取该图片，左右翻转后，侧向平移50个像素，沿顺时针方向旋转70度后保留完整的画幅尺寸，输出为JPEG格式。

如何将PIL图像转换为NumPy数组？

从以下URL导入图像并将其转换为numpy数组。
URL = ‘https://upload.wikimedia.org/wikipedia/commons/8/8b/Denali_Mt_McKinley.jpg‘

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from io import BytesIO
from PIL import Image
import PIL, requests

# Import image from URL
URL = 'https://upload.wikimedia.org/wikipedia/commons/8/8b/Denali_Mt_McKinley.jpg'
response = requests.get(URL)

# Read it as Image
I = Image.open(BytesIO(response.content))

# Optionally resize
I = I.resize([150,150])

# Convert to numpy array
arr = np.asarray(I)

# Optionaly Convert it back to an image and show
im = PIL.Image.fromarray(np.uint8(arr))

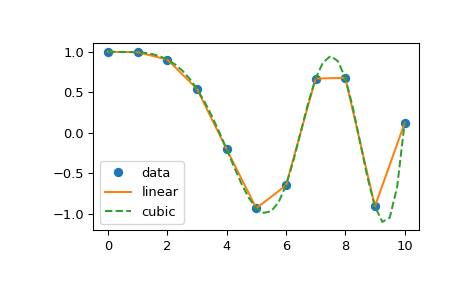
插值 (scipy.interpolate)

一维插值 (interp1d)

这个 interp1d 中的类 scipy.interpolate 是一种基于固定数据点创建函数的便捷方法，可以使用线性插值在给定数据定义的域内的任何位置计算该函数。通过传递组成数据的一维向量来创建此类的实例。此类的实例定义了一个 __call__ 方法，因此可以将其视为在已知数据值之间进行插值以获得未知值的函数(它还具有用于帮助的文档字符串)。边界处的行为可以在实例化时指定。下面的示例演示了它在线性样条插值和三次样条插值中的用法：

1
2
3
4
5
6
7
8
9
10
11
12
13
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f = interp1d(x, y)
f2 = interp1d(x, y, kind='cubic')
xnew = np.linspace(0, 10, num=41, endpoint=True)

plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic'], loc='best')
plt.show()

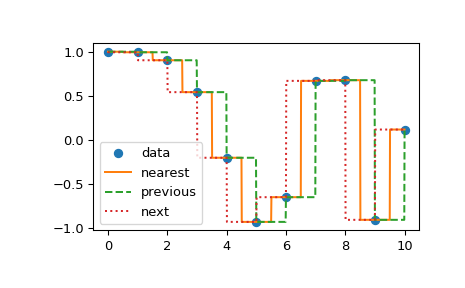
插值 interp1d 的方法常见的可以有nearest, previous以及next，其中它们返回沿x轴最近的点、上一个点或下一个点。最近的和次要的可以被认为是因果插值过滤的特例。下面的示例使用与上一个示例中相同的数据演示它们的用法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f1 = interp1d(x, y, kind='nearest')
f2 = interp1d(x, y, kind='previous')
f3 = interp1d(x, y, kind='next')
xnew = np.linspace(0, 10, num=1001, endpoint=True)

plt.plot(x, y, 'o')
plt.plot(xnew, f1(xnew), '-', xnew, f2(xnew), '--', xnew, f3(xnew), ':')
plt.legend(['data', 'nearest', 'previous', 'next'], loc='best')
plt.show()

多变量数据插值 (griddata)

例如，假设您具有基础函数的多维数据 $F(x,y)$，你只知道若干个点上的值 $[(x[i],y[i])]$，它们不会形成规则的网格。

假设我们要对二维函数 $F(x,y)$ 进行插值：

1
2
3
4
5
6
import numpy as np

def func(x, y):
    return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2

grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]

但我们只知道它在1000个数据点的值：

1
2
points = np.random.random((1000, 2))
values = func(points[:,0], points[:,1])

这可以通过以下方式完成 griddata –下面我们将尝试所有的插值方法：

1
2
3
4
5
from scipy.interpolate import griddata

grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')

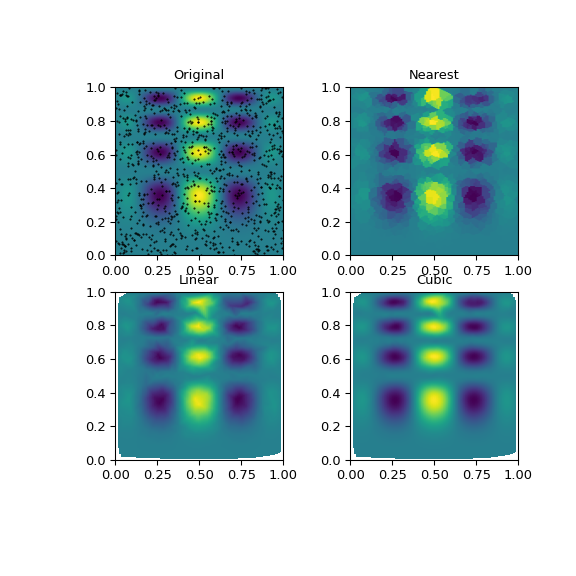
可以看到，所有方法都在一定程度上重现了准确的结果，但对于此光滑函数，三次样条插值提供了最好的结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import matplotlib.pyplot as plt
plt.subplot(221)
plt.imshow(func(grid_x, grid_y).T, extent=(0,1,0,1), origin='lower',cmap = 'hsv')
plt.plot(points[:,0], points[:,1], 'k.', ms=1)
plt.title('Original')
plt.subplot(222)
plt.imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')
plt.title('Nearest')
plt.subplot(223)
plt.imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')
plt.title('Linear')
plt.subplot(224)
plt.imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')
plt.title('Cubic')
plt.gcf().set_size_inches(6, 6)
plt.show()

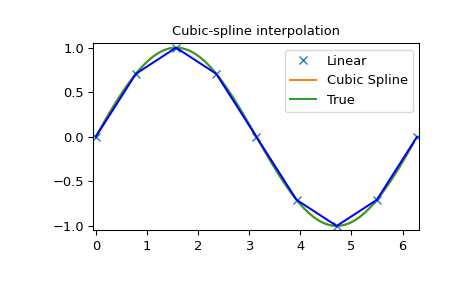
样条插值

一维中的样条插值：程序化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

# 三次样条
x = np.arange(0, 2*np.pi+np.pi/4, np.pi/4)
y = np.sin(x)
tck = interpolate.splrep(x, y, s=0)
# 求一条一维曲线的b-spline样条表示。给定一组数据点(x[i],y[i])，在有限区间上确定光滑样条近似。
# 详细信息请参照：https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.splrep.html

xnew = np.arange(0, 2*np.pi, np.pi/50)
ynew = interpolate.splev(xnew, tck, der=0)
# 求b-spline样条曲线或它的导数。给定b样条表示的结点和系数，计算平滑多项式及其导数的值。这是对FITPACK的FORTRAN例程splev和splder的包装。
# der 要计算的样条导数的阶数(必须小于或等于k，即样条的阶数)。
# 详细信息请参照：https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.splev.html

plt.figure()
plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
plt.legend(['Linear', 'Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Cubic-spline interpolation')
plt.show()

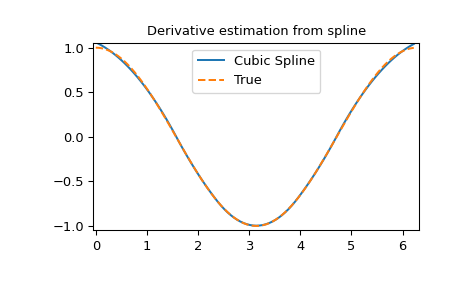
样条的导数

1
2
3
4
5
6
7
yder = interpolate.splev(xnew, tck, der=1)
plt.figure()
plt.plot(xnew, yder, xnew, np.cos(xnew),'--')
plt.legend(['Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Derivative estimation from spline')
plt.show()

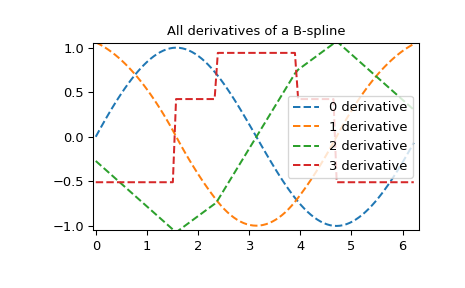
样条的所有导数

1
2
3
4
5
6
7
8
9
yders = interpolate.spalde(xnew, tck)

plt.figure()
for i in range(len(yders[0])):
   plt.plot(xnew, [d[i] for d in yders], '--', label=f"{i} derivative")
plt.legend()
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('All derivatives of a B-spline')
plt.show()

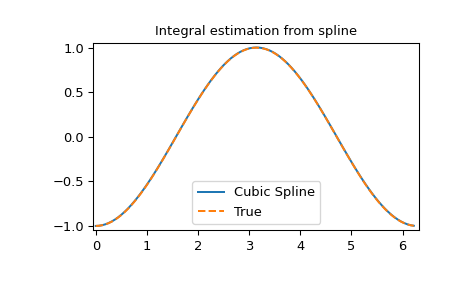
样条的积分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def integ(x, tck, constant=-1):
    x = np.atleast_1d(x)
    out = np.zeros(x.shape, dtype=x.dtype)
    for n in range(len(out)):
        out[n] = interpolate.splint(0, x[n], tck)
    out += constant
    return out
yint = integ(xnew, tck)
plt.figure()
plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
plt.legend(['Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Integral estimation from spline')
plt.show()

样条的根

1
2
interpolate.sproot(tck)
array([3.1416])

请注意， sproot 在近似区间的边缘找不到明显的解。如果我们在稍微大一点的间隔上定义样条，我们可以恢复两个根：

1
2
3
4
5
x = np.linspace(-np.pi/4, 2.*np.pi + np.pi/4, 21)
y = np.sin(x)
tck = interpolate.splrep(x, y, s=0)
interpolate.sproot(tck)
array([0., 3.1416])

参数样条

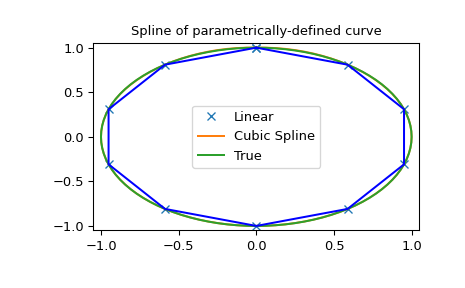
1
2
3
4
5
6
7
8
9
10
11
12
t = np.arange(0, 1.1, .1)
x = np.sin(2*np.pi*t)
y = np.cos(2*np.pi*t)
tck, u = interpolate.splprep([x, y], s=0)
unew = np.arange(0, 1.01, 0.01)
out = interpolate.splev(unew, tck)
plt.figure()
plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
plt.legend(['Linear', 'Cubic Spline', 'True'])
plt.axis([-1.05, 1.05, -1.05, 1.05])
plt.title('Spline of parametrically-defined curve')
plt.show()
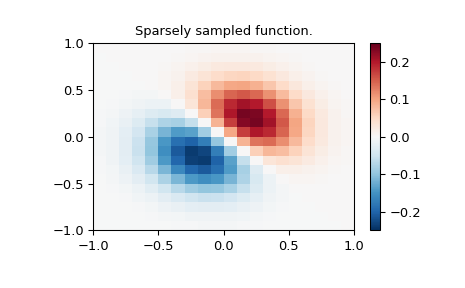
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

# 在稀疏的20x20网格上定义函数
x_edges, y_edges = np.mgrid[-1:1:21j, -1:1:21j]
x = x_edges[:-1, :-1] + np.diff(x_edges[:2, 0])[0] / 2.
y = y_edges[:-1, :-1] + np.diff(y_edges[0, :2])[0] / 2.
z = (x+y) * np.exp(-6.0*(x*x+y*y))
plt.figure()
lims = dict(cmap='RdBu_r', vmin=-0.25, vmax=0.25)
plt.pcolormesh(x_edges, y_edges, z, shading='flat', **lims)
plt.colorbar()
plt.title("Sparsely sampled function.")
plt.show()

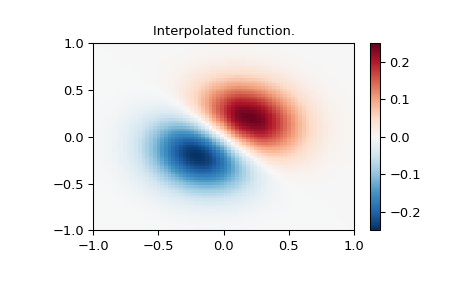
新的70x70网格上的插值函数

1
2
3
4
5
6
7
8
9
10
xnew_edges, ynew_edges = np.mgrid[-1:1:71j, -1:1:71j]
xnew = xnew_edges[:-1, :-1] + np.diff(xnew_edges[:2, 0])[0] / 2.
ynew = ynew_edges[:-1, :-1] + np.diff(ynew_edges[0, :2])[0] / 2.
tck = interpolate.bisplrep(x, y, z, s=0)
znew = interpolate.bisplev(xnew[:,0], ynew[0,:], tck)
plt.figure()
plt.pcolormesh(xnew_edges, ynew_edges, znew, shading='flat', **lims)
plt.colorbar()
plt.title("Interpolated function.")
plt.show()

随堂练习

定义一个三次二元函数，在[-10,10] x [-10,10]定义域范围内随机生成1000个点，并计算函数值。通过插值方法获取每[0.01 x 0.01]间隔的网格点处的函数值。

空间数据结构和算法 (scipy.spatial)

SciPy通过利用Qhull类库，spatial可以计算三角剖分、Voronoi图和凸包等等。此外，它还包含 KDTree 最近邻点查询的实现，以及各种度量中距离计算的实用程序。

Delaunay三角测量

Delaunay三角剖分是将一组点细分为一组不重叠的三角形，这样任何三角形的外接圆内都没有点。在实践中，这样的三角剖分往往会避免带有小角度的三角形。

可以使用以下方法计算Delaunay三角剖分 scipy.spatial 具体如下：

1
2
3
4
from scipy.spatial import Delaunay
import numpy as np
points = np.array([[0, 0], [0, 1.1], [1, 0], [1, 1]])
tri = Delaunay(points)

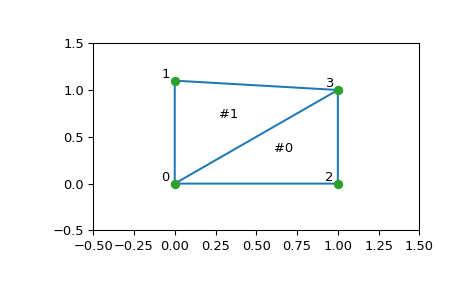
我们可以把它形象化：

1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
plt.triplot(points[:,0], points[:,1], tri.simplices)
plt.plot(points[:,0], points[:,1], 'o')

for j, p in enumerate(points):
    plt.text(p[0]-0.03, p[1]+0.03, j, ha='right') # label the points
for j, s in enumerate(tri.simplices):
    p = points[s].mean(axis=0)
    plt.text(p[0], p[1], '#%d' % j, ha='center') # label triangles
plt.xlim(-0.5, 1.5); plt.ylim(-0.5, 1.5)
plt.show()

三角剖分的结构按以下方式编码： simplices 属性包含 points 组成三角形的数组。例如：

1
2
3
4
5
6
7
8
i = 1
tri.simplices[i,:]
# array([3, 1, 0], dtype=int32)

points[tri.simplices[i,:]]
# array([[ 1. ,  1. ],
#        [ 0. ,  1.1],
#        [ 0. ,  0. ]])

此外，还可以找到相邻三角形：

1
2
tri.neighbors[i]
# array([-1,  0, -1], dtype=int32)

这告诉我们这个三角形有#0号三角形作为邻居，但没有其他邻居。此外，它还告诉我们邻居0与三角形的顶点1相对：

1
2
points[tri.simplices[i, 1]]
# array([ 0. ,  1.1])

事实上，从数字上，我们可以看到情况是这样的。

Qhull还可以对高维点集执行细分以简化(例如，在3-D中细分为四面体)。

共面点

重要的是要注意到，不是 all 由于形成三角剖分的数值精度问题，点必然显示为三角剖分的顶点。请考虑具有重复点的上述内容：

1
2
3
4
points = np.array([[0, 0], [0, 1], [1, 0], [1, 1], [1, 1]])
tri = Delaunay(points)
np.unique(tri.simplices.ravel())
array([0, 1, 2, 3], dtype=int32)

请注意，重复的点#4不会作为三角剖分的顶点出现。这件事已被记录在案：

1
2
tri.coplanar
array([[4, 0, 3]], dtype=int32)

这意味着点4位于三角形0和顶点3附近，但不包括在三角剖分中。

请注意，这种退化不仅可能是因为重复的点，也可能是由于更复杂的几何原因，即使在乍看起来表现良好的点集中也是如此。

但是，Qhull具有“qj”选项，该选项指示它随机扰乱输入数据，直到解决退化问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
tri = Delaunay(points, qhull_options="QJ Pp")
points[tri.simplices]
array([[[1, 0],
        [1, 1],
        [0, 0]],
       [[1, 1],
        [1, 1],
        [1, 0]],
       [[1, 1],
        [0, 1],
        [0, 0]],
       [[0, 1],
        [1, 1],
        [1, 1]]])

出现了两个新的三角形。然而，我们看到它们是退化的，面积为零。

凸包

凸包是包含给定点集中所有点的最小凸对象。

这些值可以通过中的qhull包装器进行计算。 scipy.spatial 具体如下：

1
2
3
4
from scipy.spatial import ConvexHull
rng = np.random.default_rng()
points = rng.random((30, 2))   # 30 random points in 2-D
hull = ConvexHull(points)

凸包被表示为一组N个1-D简化，在2-D中表示线段。存储方案与上面讨论的Delaunay三角剖分中的简化完全相同。

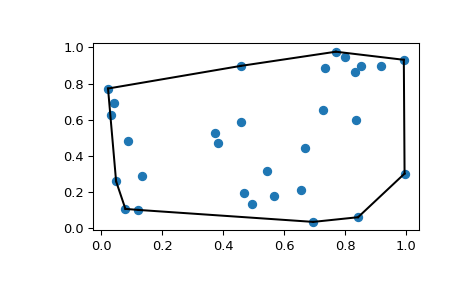
我们可以举例说明上述结果：

1
2
3
4
5
import matplotlib.pyplot as plt
plt.plot(points[:,0], points[:,1], 'o')
for simplex in hull.simplices:
    plt.plot(points[simplex,0], points[simplex,1], 'k-')
plt.show()

同样的情况也可以通过以下方式实现 scipy.spatial.convex_hull_plot_2d。

Voronoi图

Voronoi图是将空间细分为一组给定点的最近邻域。

使用以下两种方法可以接近此对象scipy.spatial 。首先，可以使用 KDTree 要回答“哪个点最接近这个点”的问题，并这样定义区域：

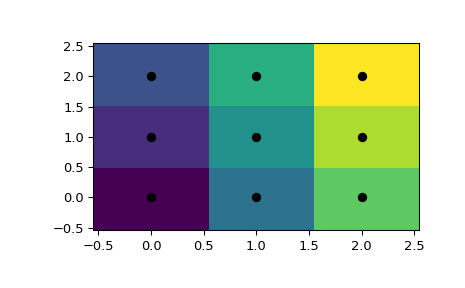
1
2
3
4
5
6
from scipy.spatial import KDTree
points = np.array([[0, 0], [0, 1], [0, 2], [1, 0], [1, 1], [1, 2],
                   [2, 0], [2, 1], [2, 2]])
tree = KDTree(points)
tree.query([0.1, 0.1])
(0.14142135623730953, 0)

所以重点是 (0.1, 0.1) 属于区域 0 。在颜色方面：

1
2
3
4
5
6
7
8
9
10
11
x = np.linspace(-0.5, 2.5, 31)
y = np.linspace(-0.5, 2.5, 33)
xx, yy = np.meshgrid(x, y)
xy = np.c_[xx.ravel(), yy.ravel()]
import matplotlib.pyplot as plt
dx_half, dy_half = np.diff(x[:2])[0] / 2., np.diff(y[:2])[0] / 2.
x_edges = np.concatenate((x - dx_half, [x[-1] + dx_half]))
y_edges = np.concatenate((y - dy_half, [y[-1] + dy_half]))
plt.pcolormesh(x_edges, y_edges, tree.query(xy)[1].reshape(33, 31), shading='flat')
plt.plot(points[:,0], points[:,1], 'ko')
plt.show()

然而，这并没有给出作为几何对象的Voronoi图。

线和点的表示可以通过中的qhull包装器再次获得 scipy.spatial：

1
2
3
4
5
6
7
from scipy.spatial import Voronoi
vor = Voronoi(points)
vor.vertices
array([[0.5, 0.5],
       [0.5, 1.5],
       [1.5, 0.5],
       [1.5, 1.5]])

Voronoi顶点表示形成Voronoi区域的多边形边的点集。在本例中，有9个不同的区域：

1
2
vor.regions
[[], [-1, 0], [-1, 1], [1, -1, 0], [3, -1, 2], [-1, 3], [-1, 2], [0, 1, 3, 2], [2, -1, 0], [3, -1, 1]]

负值 -1 再次表示无穷远处的一个点。事实上，只有一个地区， [0, 1, 3, 2]，是有界的。请注意，由于与上面的Delaunay三角剖分中类似的数值精度问题，Voronoi区域可能比输入点少。

将分隔区域的脊（二维中的线）描述为与凸面壳片类似的简化集合：

1
2
vor.ridge_vertices
[[-1, 0], [-1, 0], [-1, 1], [-1, 1], [0, 1], [-1, 3], [-1, 2], [2, 3], [-1, 3], [-1, 2], [1, 3], [0, 2]]

这些数字表示组成线段的Voronoi顶点的索引。 -1 又是一个无穷远的点-12条直线中只有4条是有界线段，而其他的延伸到无穷远。

Voronoi山脊垂直于输入点之间绘制的线。还记录了每个脊对应的两个点：

1
2
3
4
5
6
7
8
9
10
11
12
13
vor.ridge_points
array([[0, 3],
       [0, 1],
       [2, 5],
       [2, 1],
       [1, 4],
       [7, 8],
       [7, 6],
       [7, 4],
       [8, 5],
       [6, 3],
       [4, 5],
       [4, 3]], dtype=int32)

这些信息加在一起，足以构成完整的图表。

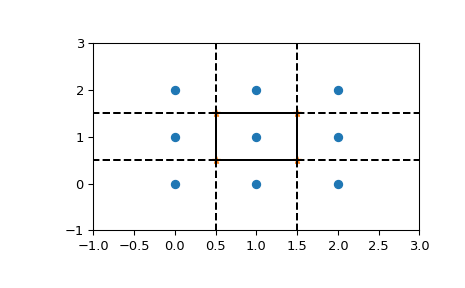
我们可以把它画成如下图。首先，点和Voronoi顶点：

1
2
3
plt.plot(points[:, 0], points[:, 1], 'o')
plt.plot(vor.vertices[:, 0], vor.vertices[:, 1], '*')
plt.xlim(-1, 3); plt.ylim(-1, 3)

绘制有限线段与绘制凸壳一样，但现在我们必须注意无限边：

1
2
3
4
for simplex in vor.ridge_vertices:
    simplex = np.asarray(simplex)
    if np.all(simplex >= 0):
        plt.plot(vor.vertices[simplex, 0], vor.vertices[simplex, 1], 'k-')

延伸到无穷远的山脊需要稍微小心一点：

1
2
3
4
5
6
7
8
9
10
11
12
13
center = points.mean(axis=0)
for pointidx, simplex in zip(vor.ridge_points, vor.ridge_vertices):
    simplex = np.asarray(simplex)
    if np.any(simplex < 0):
        i = simplex[simplex >= 0][0] # finite end Voronoi vertex
        t = points[pointidx[1]] - points[pointidx[0]]  # tangent
        t = t / np.linalg.norm(t)
        n = np.array([-t[1], t[0]]) # normal
        midpoint = points[pointidx].mean(axis=0)
        far_point = vor.vertices[i] + np.sign(np.dot(midpoint - center, n)) * n * 100
        plt.plot([vor.vertices[i,0], far_point[0]],
                 [vor.vertices[i,1], far_point[1]], 'k--')
plt.show()

也可以使用以下命令创建此图 scipy.spatial.voronoi_plot_2d 。

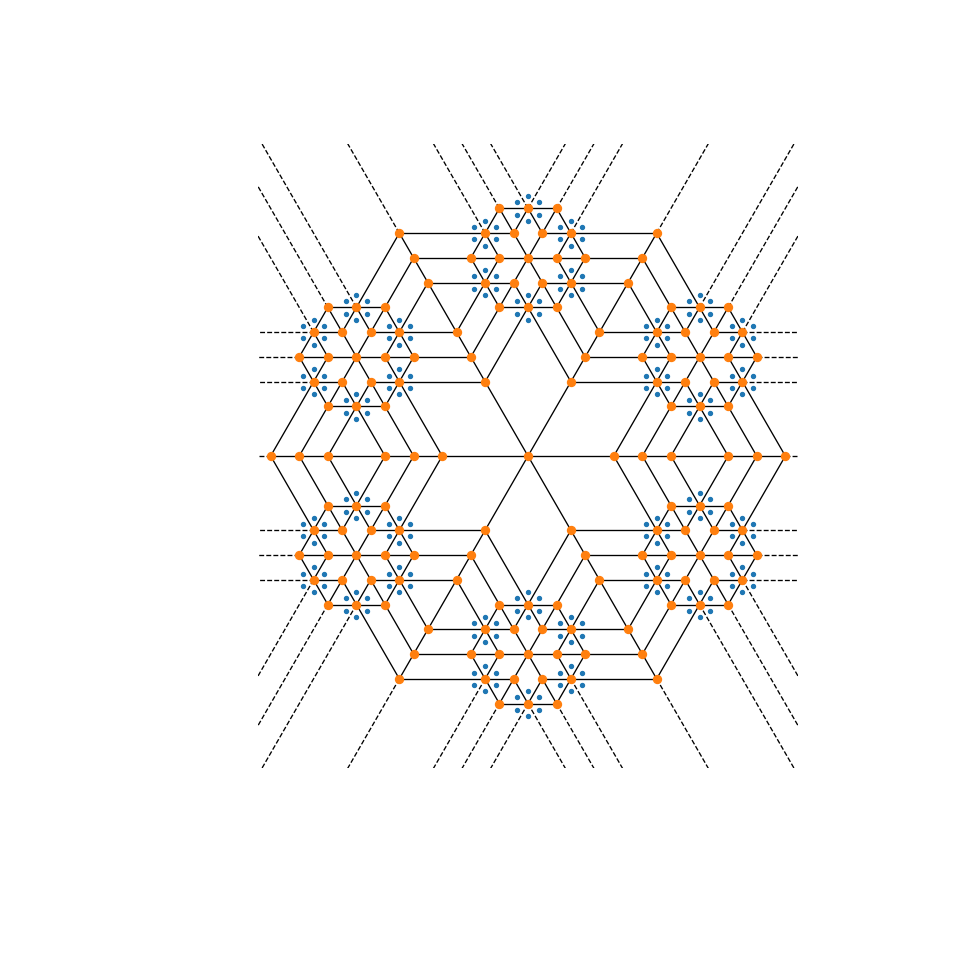
Vornoi图可以用来创作有趣的创作艺术。尝试使用此设置 mandala 函数来创建您自己的！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import numpy as np
from scipy import spatial
import matplotlib.pyplot as plt
def mandala(n_iter, n_points, radius):
    """Creates a mandala figure using Voronoi tesselations.

    Parameters
    ----------
    n_iter : int
        Number of iterations, i.e. how many times the equidistant points will
        be generated.
    n_points : int
        Number of points to draw per iteration.
    radius : scalar
        The radial expansion factor.

    Returns
    -------
    fig : matplotlib.Figure instance

    Notes
    -----
    This code is adapted from the work of Audrey Roy Greenfeld [1]_ and Carlos
    Focil-Espinosa [2]_, who created beautiful mandalas with Python code.  That
    code in turn was based on Antonio Sánchez Chinchón's R code [3]_.

    References
    ----------
    .. [1] https://www.codemakesmehappy.com/2019/09/voronoi-mandalas.html

    .. [2] https://github.com/CarlosFocil/mandalapy

    .. [3] https://github.com/aschinchon/mandalas

    """
    fig = plt.figure(figsize=(10, 10))
    ax = fig.add_subplot(111)
    ax.set_axis_off()
    ax.set_aspect('equal', adjustable='box')

    angles = np.linspace(0, 2*np.pi * (1 - 1/n_points), num=n_points) + np.pi/2
    # Starting from a single center point, add points iteratively
    xy = np.array([[0, 0]])
    for k in range(n_iter):
        t1 = np.array([])
        t2 = np.array([])
        # Add `n_points` new points around each existing point in this iteration
        for i in range(xy.shape[0]):
            t1 = np.append(t1, xy[i, 0] + radius**k * np.cos(angles))
            t2 = np.append(t2, xy[i, 1] + radius**k * np.sin(angles))

        xy = np.column_stack((t1, t2))

    # Create the Mandala figure via a Voronoi plot
    spatial.voronoi_plot_2d(spatial.Voronoi(xy), ax=ax)

    return fig
# Modify the following parameters in order to get different figures
n_iter = 3
n_points = 6
radius = 4
fig = mandala(n_iter, n_points, radius)
plt.show()